可持久化线段树

可持久化线段树

一月 16, 2022

前置知识

线段树、离散化、可持久化概念、二分

问题引入

这里我们就用最简单的静态求区间第k小数问题来引入，谷站链接：P3834 【模板】可持久化线段树 2。

这里简单描述一下题目：
有一组数量为$n(n\le2e5)$的数据（每个数$num\le1e9$），$m(m\le1e9)$次询问，每次询问该数据中编号为$[l,r]$区间中的第$k$小数，这里的编号从1开始，$k$也从1开始

思考过程

首先，我们可以发现这个问题是一个区间查询问题，可以想到要用线段树这种数据结构来维护，但如果简单地用线段树去维护原先的数组，“第$k$小数”这个信息并不能很好地维护，且不能通过子节点来推出父节点的信息。那我们可以转变一下思路，在这个问题中我们关注的并不是这个数本身的大小，而是这个数在某一区间当中的排名，所以只要维护区间上数的大小关系即可，那么通过离散化我们可以将答案限制在一个较小的范围内，显然，这样的情况是很适合二分的，并且我们可以注意到线段树本身便是对区间的一种二分处理。那么我们可以对线段树做一个改造，不去维护原来的数据，而是维护我们的答案范围，并同时记录每个区间上有多少个离散化后的读入数据。这样对于每一次询问，我们只需要从线段树的根节点开始，先看左儿子上拥有的数的个数（记为$sum$），如果大于等于$k$，那么我们的答案就必然在左儿子所维护的区间内部；而如果小于$k$,答案便在右儿子的区间内部，并且为右儿子区间上拥有的数中的第$k-sum$个数，如此递归查询，直达达到叶节点，便能确定我们的答案了。

然而如果只是这样的话，我们并不能保证$sum$中的每一个数的下标都在$[l,r]$之间，所以$sum$是大于等于真实值的，这便要求我们的数据结构可以维护每一次加入一个数前后的线段树上的节点信息情况，而这就是“可持久化”的用武之地了，这个数据结构也就是我们今天的主角——可持久化线段树

介绍

综上所述，可持久化线段树并不是普通的区间维护线段树，而是一颗权值线段树。可持久化这一概念就不多赘述了（可以参考链接中OI Wiki的描述），也就是对读入的每个数进行动态开点，先复制上一版本的信息，然后再新建一些点保留这次更新的信息，由于每次的都加入一个点，且树高为$\log_2n$，那么每次会更改不超过树高的点，单次开点的复杂度便是$O(\log n)$。如果对这个过程有不理解的话，我的建议是（1）在纸上画一次开点的过程，模拟一下；（2）看代码来协助理解。
这里加（盗）一张图，来便于理解。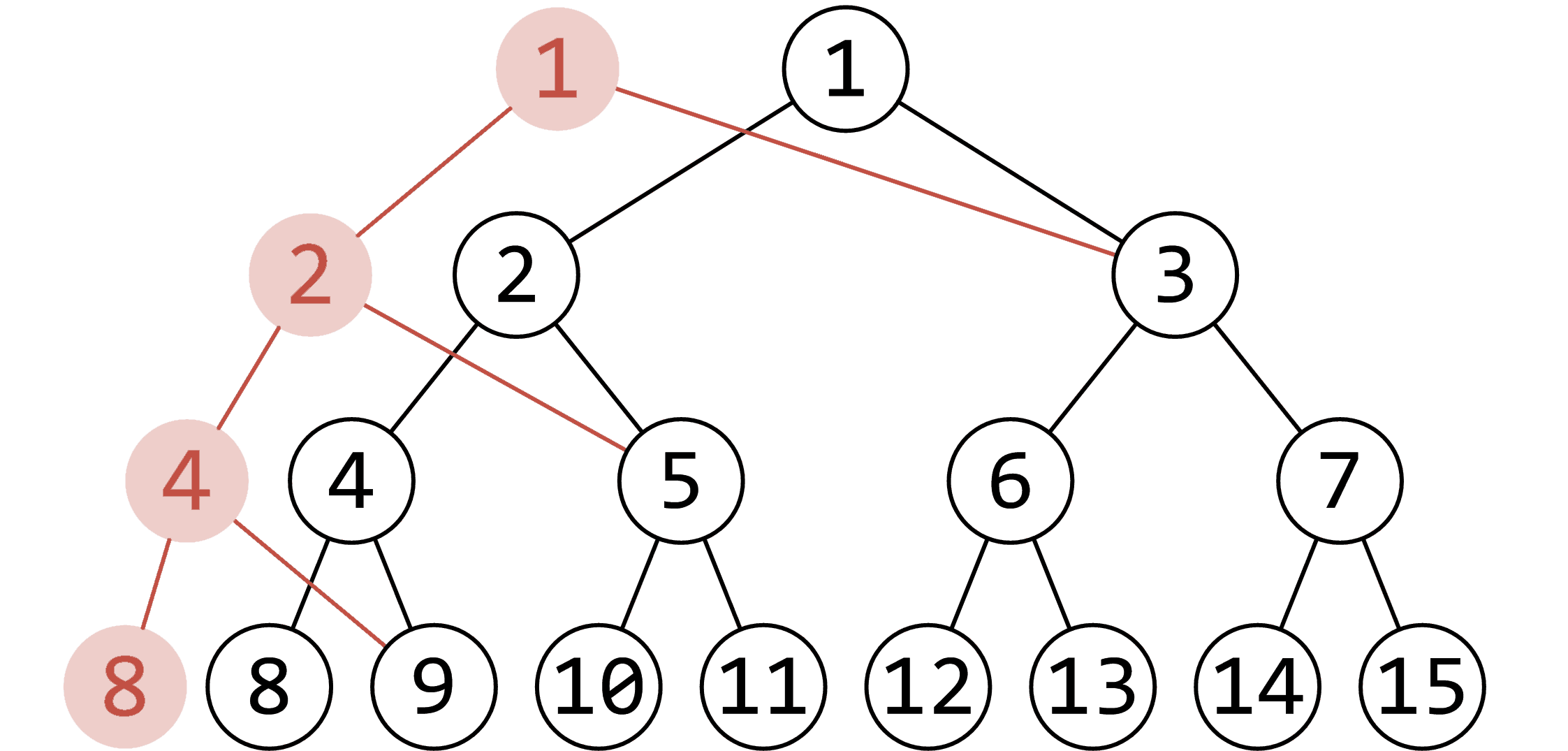
persistent_segment_tree

代码（带注释）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<vector>
using namespace std;
typedef long long ll;
const int N=2e5+10;
int idx;//记录当前节点编号
int root[N];//记录每个版本的根
vector<int> a;//用于离散化
int c[N];//存储原数据
//这里节点并不维护其表示的区间的左右端点，而是通过过程中计算得到
struct Node{
    int ls,rs;//分别代表左、右儿子的编号
    int cnt;//节点区间中拥有的数
}tr[N*18];//这里的空间为NlogN，如果要加建树则要加上4*N的空间
//这道题由于是动态开点，所以是不需要建树的（建树的话是没有初始信息的）
int find(int x){
    return lower_bound(a.begin(),a.end(),x)-a.begin();
}//通过原来的数查询离散化后对应的数
void pushup(int p){
    tr[p].cnt=tr[tr[p].ls].cnt+tr[tr[p].rs].cnt;
}//子节点更新父节点信息
/*没用的建树还是写一下。。
int build(int l,int r){
    int q=++idx;
    int mid=(l+r)>>1;
    tr[q].ls=build(l,mid);
    tr[q].rs=build(mid+1,r);
    pushup(q);
    return q；
}
*/
int insert(int p,int l,int r,int x){
    int q=++idx;
    tr[q]=tr[p];
    if(l==r){
        tr[q].cnt++;
        return q;
    }
    int mid=(l+r)>>1;
    if(x<=mid)tr[q].ls=insert(tr[p].ls,l,mid,x);
    else tr[q].rs=insert(tr[p].rs,mid+1,r,x);
    pushup(q);
    return q;
}//动态开点，p为上一版本对应的点的编号，q先复制上一版本信息，再更新信息，最后返回新点的序号
int query(int p,int q,int l,int r,int k){
    int sum=tr[tr[q].ls].cnt-tr[tr[p].ls].cnt;
    if(l==r){
        return r;
    }
    int mid=(l+r)>>1;
    if(sum>=k)return query(tr[p].ls,tr[q].ls,l,mid,k);
    else return query(tr[p].rs,tr[q].rs,mid+1,r,k-sum);
}//查询操作
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        scanf("%d",&c[i]);
        a.push_back(c[i]);
    }
    sort(a.begin(),a.end());
    a.erase(unique(a.begin(),a.end()),a.end());
    //root[0]=build(0,a.size()-1)；没用的建树。。
    //保序离散化
    //注意a是以0开始标号的
    for(int i=1;i<=n;i++){
        root[i]=insert(root[i-1],0,a.size()-1,find(c[i]));//逐一开点
    }
    while(m--){
        int l,r,k;
        scanf("%d%d%d",&l,&r,&k);
        int ans=a[query(root[l-1],root[r],0,a.size()-1,k)];//在区间[l,r]中查询第k小
        //注意（1）类似前缀和，查询的是l-1和r，（2）查询结果为离散化后的值，需要还原
        printf("%d\n",ans);
    }
    return 0;
}

  1. 1. 前置知识
  2. 2. 问题引入
  3. 3. 思考过程
  4. 4. 介绍
  5. 5. 代码（带注释）